Twins Paradox in Relativity
in absolute terms
with a twins paradox animation
Roger Luebeck © 2008, 2011, 2024
The preprint of my journal article is at this link: preprint.special_relativity.pdf
Also see my tutorial for computing non-kinematical and kinematical time-keeping dilation, with commentary on the Hafele-Keating study of circumnavigating jets: time-dilation.pdf
You have just stumbled into the sole source for diagrams, derivations and animations in absolute terms for symmetry of measure and time-keeping contraction in special relativity.
See site map for all my articles.
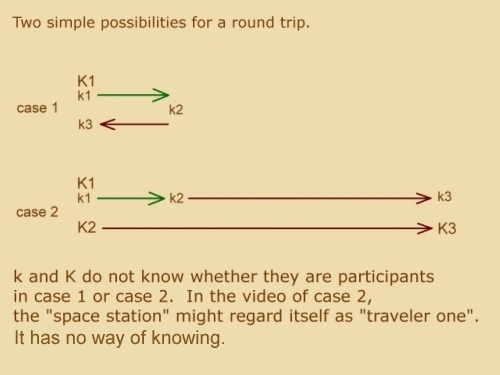
The illustration above and the two-part animation below illustrate two basic possibilities for completing a round trip between two parties. They produce identical kinematical time-keeping differentials, demonstrating the impossibility of anyone determining their true motion status relative to the universe.
That is - none of the parties involved can assume anything about their actual state of motion; thus they cannot know whether they are participating in case 1 or case 2.
For maximum clarity, the trips themselves involve just a light second or two in distance, and all parties make use of photon clocks that are a whopping 1/2 light second in width. The photon clocks tell the story of time contraction.
The horizontal white lines represent the travelers. They each carry a photon clock. And again, the fact that time differential is identical in both scenarios confirms that one cannot experimentally detect one's true motion status relative to the universe.
Scenario 1:
In part one of the twins paradox animation below, an astronaut and a space station occupant start their clocks as the astronaut passes by. A second, incoming, astronaut starts his clock as he passes by the first astronaut. The incoming astronaut and the space station occupant stop their clocks as the incoming astronaut passes by the space station.
Scenario 2:
In part two of the twins paradox animation below, an astronaut and a space station occupant start their clocks as the astronaut passes by. A second, also outbound, astronaut starts his clock as he passes by the space station. This second astronaut chases down the first astronaut. As the first astronaut is caught, both astronauts stop their clocks.
In scenario 2, one needs to abandon the strict labels of "space station", "traveler one" and "traveler two", even though the video labels them as such for simplicity. In scenario 2, the "space station" might regard itself as "traveler one" who meets "traveler two" coming from what the "space station" regards as the opposite direction of travel. The parties involved have no way of knowing which scenario they are involved in.
In February of 2024, sixteen years after writing my book explaining special relativity in absolute terms, I stumbled into an obscure lecture Einstein had delivered at Leyden in 1920 wherein he forcefully argued for the pertinence of the structure of space in special relativity. That was fifteen years after producing his special theory of relativity. His initial treatment, in 1905, was absent of any consideration of space as the backdrop for motion; and that initial treatment is the one still wrongly embraced by the physics community at large.
The totality of the universe -- in strict accordance with the reasoning of Mach and others -- imparts inertial properties
(length and kinematical clock-rate) to everything it contains.
Einstein stated at Leyden in 1920:
"Mach's idea finds its full development in the ether of General Relativity" and "Space without ether is unthinkable; for in such space there .. would be .. no possibility of existence for standards of space and time, [specifically] our measuring-rods and clocks, nor therefore any [space or time] intervals in the physical sense."
However, Einstein never went back and reworked special relativity in absolute terms.
Yes, the relativity of Lorentz, Poincare and Fitzgerald have been around for as long as Einstein's relativity. However, their treatments lack convincing natural postulates, any definition of time-keeping, or any diagramming of measuring processes across inertial frames.
These things I did in Relativity Trail, and more concisely at:
preprint.special_relativity.pdf
Also see: Einstein at Leyden
-----------------------------------------------------------------------
The time contraction formula is easily obtained from the above diagrams. For instance, in the first diagram (animation), the clock at rest with the universe ticks off one cycle while the traveling clock ticks off 0.8 of a cycle. A simple application of the Pythagorean Theorem yields the following formula:
t' = t ( 1 - V^2 ) ^ 1/2
where t' is the time recorded by the traveler, t is universal time (full clock rate, since at rest with the universe), and v is the speed of the traveler.
Keep in mind that the traveler, moving at 0.6 light second per second of universal time, went a distance, in absolute terms, of 0.6 light second.
A photon went the same distance in the station's clock as it did in the traveler's clock, namely, 1 light second.
Thus,
0.8 = ( 1 - 0.6^2) ^ 1/2
= ( 1 - 0.36) ^ 1/2
= ( 0.64 ) ^ 1/2
= 0.8
(There is no need to use c (light speed) in the equation, since we are using units of light seconds. Light travels one light second in one second.)
© 2008, 2011, 2024 Roger Luebeck
Updated 03/13/2025
site map
The preprint of my journal article is at this link: preprint.special_relativity.pdf
Also see my tutorial for computing non-kinematical and kinematical time-keeping dilation, with commentary on the Hafele-Keating study of circumnavigating jets: time-dilation.pdf
You have just stumbled into the sole source for diagrams, derivations and animations in absolute terms for symmetry of measure and time-keeping contraction in special relativity.
See site map for all my articles.
The illustration above and the two-part animation below illustrate two basic possibilities for completing a round trip between two parties. They produce identical kinematical time-keeping differentials, demonstrating the impossibility of anyone determining their true motion status relative to the universe.
That is - none of the parties involved can assume anything about their actual state of motion; thus they cannot know whether they are participating in case 1 or case 2.
For maximum clarity, the trips themselves involve just a light second or two in distance, and all parties make use of photon clocks that are a whopping 1/2 light second in width. The photon clocks tell the story of time contraction.
The horizontal white lines represent the travelers. They each carry a photon clock. And again, the fact that time differential is identical in both scenarios confirms that one cannot experimentally detect one's true motion status relative to the universe.
Scenario 1:
In part one of the twins paradox animation below, an astronaut and a space station occupant start their clocks as the astronaut passes by. A second, incoming, astronaut starts his clock as he passes by the first astronaut. The incoming astronaut and the space station occupant stop their clocks as the incoming astronaut passes by the space station.
Scenario 2:
In part two of the twins paradox animation below, an astronaut and a space station occupant start their clocks as the astronaut passes by. A second, also outbound, astronaut starts his clock as he passes by the space station. This second astronaut chases down the first astronaut. As the first astronaut is caught, both astronauts stop their clocks.
In scenario 2, one needs to abandon the strict labels of "space station", "traveler one" and "traveler two", even though the video labels them as such for simplicity. In scenario 2, the "space station" might regard itself as "traveler one" who meets "traveler two" coming from what the "space station" regards as the opposite direction of travel. The parties involved have no way of knowing which scenario they are involved in.
In February of 2024, sixteen years after writing my book explaining special relativity in absolute terms, I stumbled into an obscure lecture Einstein had delivered at Leyden in 1920 wherein he forcefully argued for the pertinence of the structure of space in special relativity. That was fifteen years after producing his special theory of relativity. His initial treatment, in 1905, was absent of any consideration of space as the backdrop for motion; and that initial treatment is the one still wrongly embraced by the physics community at large.
The totality of the universe -- in strict accordance with the reasoning of Mach and others -- imparts inertial properties
(length and kinematical clock-rate) to everything it contains.
Einstein stated at Leyden in 1920:
"Mach's idea finds its full development in the ether of General Relativity" and "Space without ether is unthinkable; for in such space there .. would be .. no possibility of existence for standards of space and time, [specifically] our measuring-rods and clocks, nor therefore any [space or time] intervals in the physical sense."
However, Einstein never went back and reworked special relativity in absolute terms.
Yes, the relativity of Lorentz, Poincare and Fitzgerald have been around for as long as Einstein's relativity. However, their treatments lack convincing natural postulates, any definition of time-keeping, or any diagramming of measuring processes across inertial frames.
These things I did in Relativity Trail, and more concisely at:
preprint.special_relativity.pdf
Also see: Einstein at Leyden
-----------------------------------------------------------------------
The time contraction formula is easily obtained from the above diagrams. For instance, in the first diagram (animation), the clock at rest with the universe ticks off one cycle while the traveling clock ticks off 0.8 of a cycle. A simple application of the Pythagorean Theorem yields the following formula:
t' = t ( 1 - V^2 ) ^ 1/2
where t' is the time recorded by the traveler, t is universal time (full clock rate, since at rest with the universe), and v is the speed of the traveler.
Keep in mind that the traveler, moving at 0.6 light second per second of universal time, went a distance, in absolute terms, of 0.6 light second.
A photon went the same distance in the station's clock as it did in the traveler's clock, namely, 1 light second.
Thus,
0.8 = ( 1 - 0.6^2) ^ 1/2
= ( 1 - 0.36) ^ 1/2
= ( 0.64 ) ^ 1/2
= 0.8
(There is no need to use c (light speed) in the equation, since we are using units of light seconds. Light travels one light second in one second.)
© 2008, 2011, 2024 Roger Luebeck
Updated 03/13/2025
site map